5 Leistungsverstärker
Lernziele
- Auslegung von analogen Schaltungen
- Strukturiertes aufbereiten einer Aufgabenstellung
- Plausibilität und Qualitätsbeurteilung mittels Simulation
- Übersichtliches zeichnen komplexer Schaltpläne
- Strukturiertes, Zeitoptimiertes Dokumentieren der Arbeit
Transistorverstärker, wie sie bisher bekannt sind Kapitel 4.2, in denen ein Transistor in einem Arbeitspunkt betrieben wird, haben bei höheren Leistungen eine zu hohe Verlustleistung. Die Verlustleistung ist proportional zum Strom durch den Kollektor \(I_C\) in Ruhe, also ohne Signal am Eingang. Bei der Emitterschaltung ist der Ruhestrom höher, da der Arbeitspunkt auf der Kennlinie weiter “oben” ist. Diese Betriebsart wird auch A - Betrieb genannt.
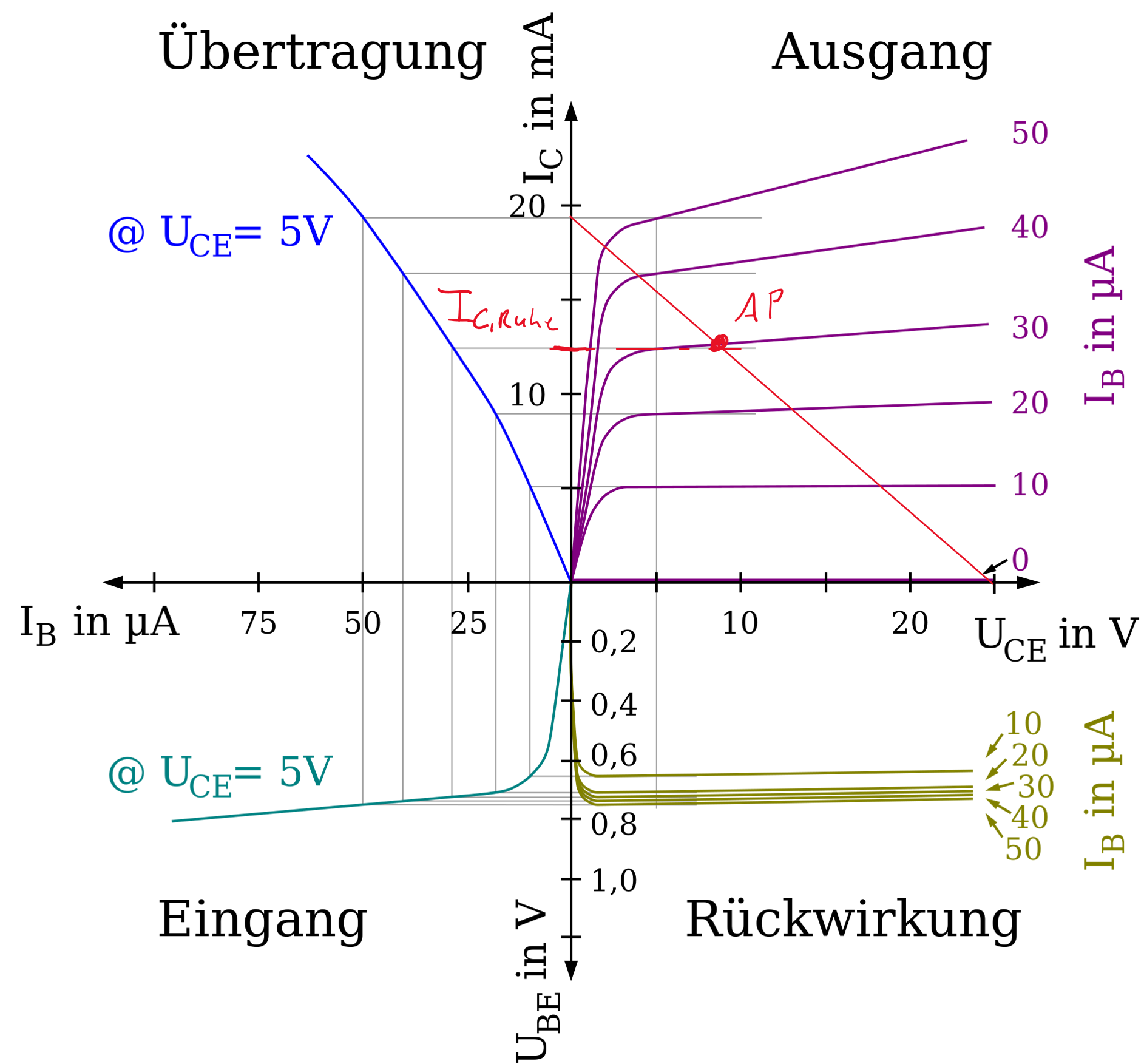
Um höhere Leistungen und eine geringere Verlustleistung zu erreichen, muss der Arbeitspunkt nach “unten”, also zu einem kleineren \(I_C\) gebracht werden. Wird dies am Beispiel des Verstärkers in Emittergrundschaltung Kapitel 4.2 gemacht, würde das bedeuten, dass nur noch eine Halbwelle verstärkt wird. Um dies zu verhindern, werden ein PNP und ein NPN Transistor in Gegentakt geschaltet. Jeder Transistor übernimmt nun die Verstärkung einer Halbewelle. Warum der \(I_C\), und damit die Verlustleistung, trotzdem nicht ganz Null sein kann, sehen wir im folgenden Teil.
5.1 Die Gegentaktendstufe
Um zu vermeiden, dass der Arbeitspunkt eine höhere Verlustleistung aufgrund eines höheren \(I_C\) verursacht, und trotzdem ein symmetrisches Signal verstärkt werden kann, können zwei Transistoren eingesetzt werden. Damit ist auch die maximale Leistung höher, da der Arbeitsbereich pro Transistor besser ausgenutzt wird. Ein Transistor verstärkt die positiven Signale. Der andere die negativen. Dies wird Gegentaktendstufe genannt. Die Betriebsart wird hier als B bezeichnet. Wird eine reale Schaltung entwickelt, ist stets darauf zu achten, dass die Bauteileigenschaften berücksichtigt werden. Speziell die Maximalwerte dürfen nicht überschritten werden.
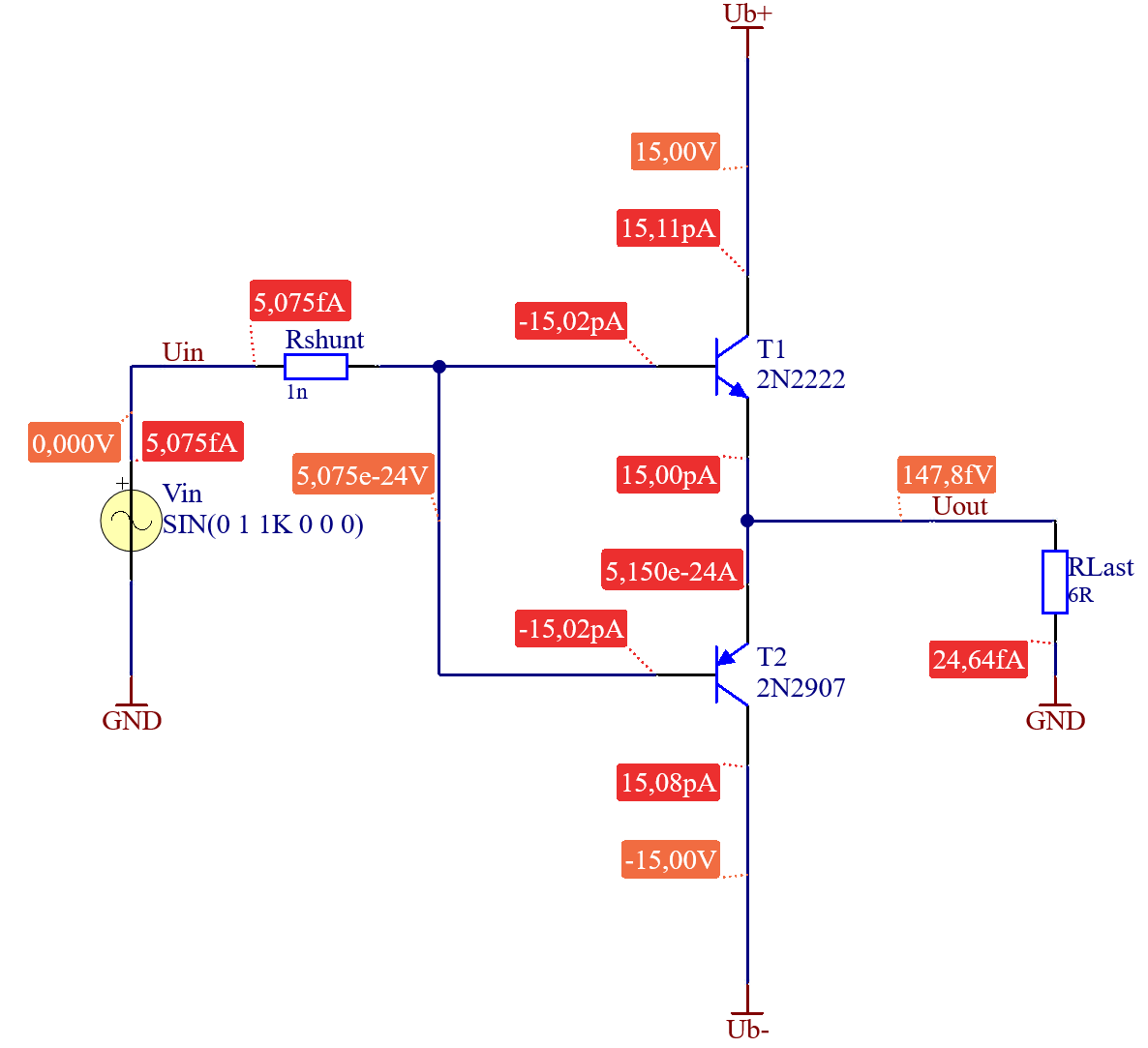
Wird diese Schaltung einem Test unterzogen, zeigt sich, dass das Ergebnis wenig zufriedenstellend ist. Weder wird die Amplitude erreicht, das Signal wird gedämpft, noch folgt der Ausgang dem sinusförmigen Verlauf des Eingangs. Speziell an den Nulldurchgängen gibt es beträchtliche Verzerrungen. Als Qualitätskriterium soll von nun an die Differenz zwischen Ausgangsspannung und Eingangsspannung herangezogen werden.
| Simulationsparameter | Wert | Bemerkung |
|---|---|---|
| \(V_{in}\) Frequenz | 1 kHz | |
| \(V_{in}\) Amplitude | 1 V | |
| Simulierte Perioden | 3 |
5.2 Rückkopplung
Um den Verlauf der Ausgangsspannung an den Verlauf der Eingangsspannung anzupassen, wird eine Gegenkopplung verwendet. Dazu ist eine Subtraktion des Ausgangssignals vom Eingangssignal notwendig. Als Transistorschaltung würde sich eine Differenzverstärkerschaltung anbieten. Für ein noch besseres Ergebnis wird hier ein OPV eingesetzt. Durch die Rückkopplung der gesamten Ausgangsspannung wird eine Spannungsverstärkung von Eins erreicht. Das Ausgangssignal folgt dem Eingangssignal. Eine legitime Frage ist, warum nicht einfach nur der OPV verwendet wird? Hier kann auf die Überschrift verwiesen werden. Es soll Leistung verstärkt werden. Und die Ausgangsleistung eines OPV reicht in der Regel nicht aus, um beispielsweise einen Lautsprecher zu betreiben.
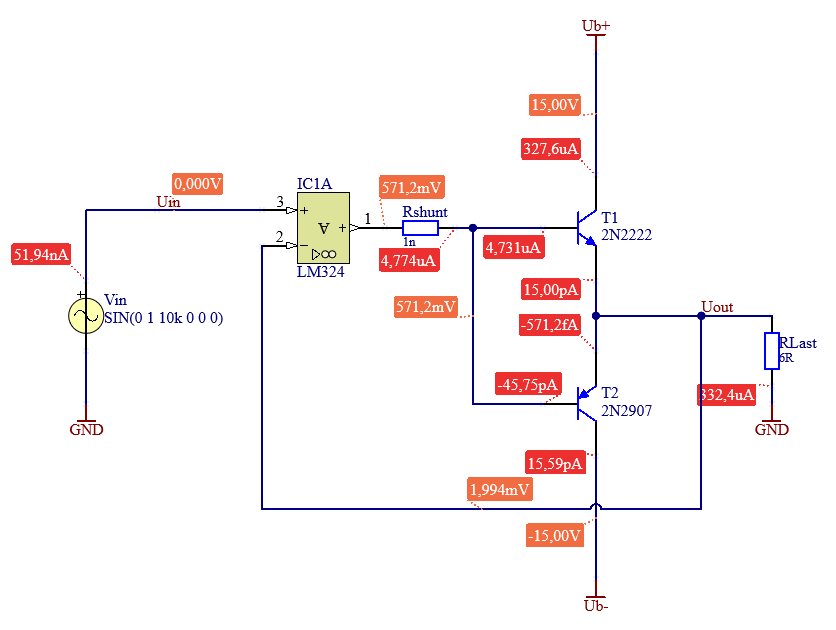
Mittels Simulation kann nun erneut die Qualität überprüft werden. Es ist zu erkennen, dass die Amplitude erreicht wird. An den Nulldurchgängen sind jedoch noch Störungen zu sehen. Die Ursache dieser Störungen sind die Kennlinien der Transistoren. In Abbildung 5.1 lässt sich erkennen, dass sich in der Nähe des Ursprunges ein Knick befindet. Erst ab einer \(U_{BE} \ \) größer von ca. \(0,7 \ \mathrm{V}\) beginnt der Transistor zu leiten. Das bedeutet, dass Eingangssignale kleiner als diese minimal notwendige Basis- Emitterspannung nicht verstärkt werden.
Der OPV wirkt zwar auch den Übergabeverzerrungen entgegen, allerdings ist er stark abhängig von der Frequenz. Je schneller im Verhältnis zum Signal der OPV sein Ausgangssignal ändern kann, umso kleiner sind die Verzerrungen. Wie schnell der OPV seinen Ausgang ändern kann, hängt von der Slew-Rate mit der Einheit \(\mathrm{\frac{V}{s}}\) ab.
| Simulationsparameter | Wert | Bemerkung |
|---|---|---|
| \(V_{in}\) Frequenz | 10 kHz | |
| \(V_{in}\) Amplitude | 1 V | |
| Simulierte Perioden | 3 |
5.3 Vorspannen
Um die Übergabeverzerrungen zu eliminieren wird die B-E Strecke vorgespannt. Das bedeutet eine Spannung anzulegen, welche größer ist als die Schwellspannung der Basis- Emitter Strecke. Damit ist der Transistor bereits im leitenden Bereich und wird nur noch vom Eingangssignal weiter ausgesteuert.
Da durch das Vorspannen auch ein Kollektorstrom durch den Transistor fließt, wenn am Eingang \(0 \ \mathrm{V} \ \) anliegen erhöhen sich die Verluste. Dieser Kollektorstrom wird auch als Ruhestrom bezeichnet \(I_{C,Ruhe} \ \). Um den Ruhestrom möglichst klein zu halten, muss die Spannungsquelle an die Transistoren und deren Fertigungstoleranzen angepasst werden.
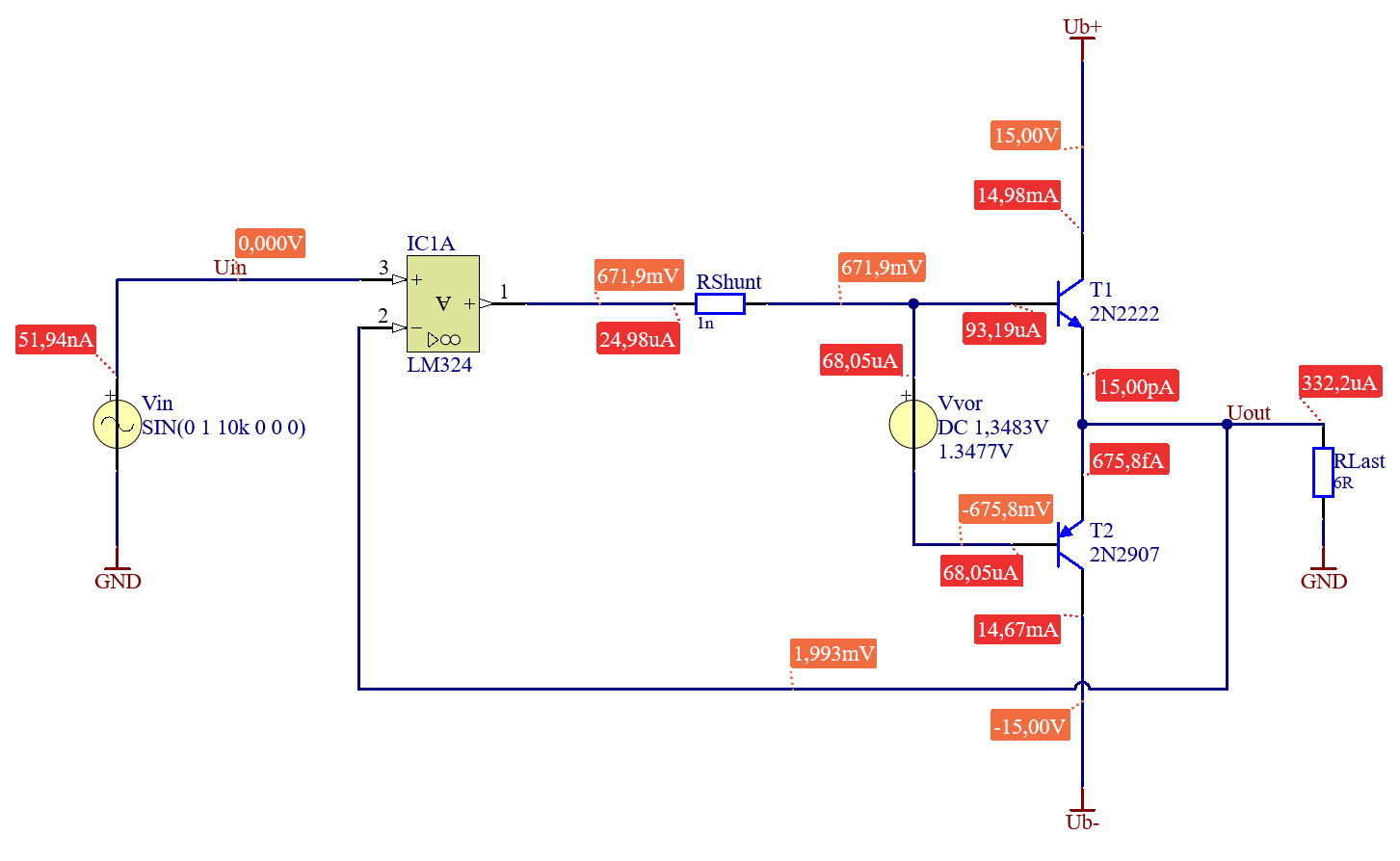
Mittels DC-Sweep kann die Spannungsquelle auf einen gewünschten \(I_C\) eingestellt werden. Der \(I_C\) ist so zu wählen, dass der Arbeitspunkt außerhalb des nichtlinearen Bereichs der Transistorkennlinie liegt. Gleichzeitig soll er so klein wie möglich sein, um die Verluste gering zu halten. Hier soll der \(I_C\) ein Zehntel des maximalen Laststromes betragen.
| Simulationsparameter | Wert | Bemerkung |
|---|---|---|
| \(V_{vor}\) min | 1 V | |
| \(V_{vor}\) max | 1,4 V | |
| \(V_{vor}\) step size | 10 mV |
Mit dem Cursor können die Ergebnisse exakt abgelesen werden.
| Simulationsergebnis | Wert | Bemerkung |
|---|---|---|
| \(V_{vor}\) bei \(I_C\) = 15 mA an T1 | 1,3479 V | |
| \(V_{vor}\) bei \(I_C\) = 15 mA an T2 | 1,3488 V |
Da es sich um unterschiedliche Transistoren handelt, ist natürlich auch der Zusammenhang zwischen \(U_{BE}\) und \(I_C\) ein anderer. Da die Werte sehr nahe beieinander liegen, kann ein gerundetes arithmetisches Mittel als Ergebnis für \(V_{Vor}\) verwendet werden.
Der Verstärker hat nun eine Qualität, welche das Verstärken von niederfrequenten Signalen in ausreichender Güte erlaubt, um beispielsweise Musik zu verstärken. Dies ist am geringen Unterschied zwischen der Eingangsspannung und der Ausgangsspannung zu erkennen.
| Simulationsparameter | Wert | Bemerkung |
|---|---|---|
| \(V_{in}\) Frequenz | 10 kHz | |
| \(V_{in}\) Amplitude | 1 V | |
| Simulierte Perioden | 3 |
Welche anderen Darstellungen des Verhältnisses zwischen Ausgang und Eingang würden sich eignen um nachzuweisen, dass die Verzerrung akzeptabel ist?
5.4 Reale Spannungsquelle
Ideale Spannungsquellen, wie oben eingezeichnet, existieren nicht. Daher muss die ideale Spannungsquelle mit einer realen Spannungsquelle ersetzt werden. Aus Kostengründen muss dies mit möglichst wenigen Bauteilen geschehen. Daher fällt ein Netzteil aus. Eine Schaltung mit nur drei Bauteilen, welche die Aufgabe erledigen kann, ist ein sogenannter “\(U_{BE}\)-Vervielfacher” [2, pp. 301].
In Abbildung 5.9 wird die Schaltung gezeigt. Um die Schaltung zu dimensionieren, kann der \(U_{BE}\)-Vervielfacher alleine betrachtet werden. \(U_{out}\) ist aus Kapitel 5.3 bekannt. Es müssen nun also die Widerstände \(R_{sq1}\) und \(R_{sq2}\) so dimensioniert werden.
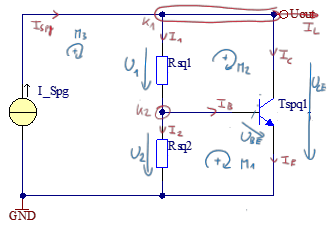
Der Ablauf ist wie folgt und gilt für alle Dimensionierungsaufgaben von Schaltungen.
5.4.1 \(U_{BE}\)-Vervielfacher berechnen.
Dabei wird die Schaltung analytisch, also mit Formeln berechnet.
Es soll, wie bei der Dimensionierung der Emitterverstärkerschaltung, klar gekennzeichnet werden, woher die Formeln und Werte kommen.
Gesucht wird \(R_{sq1}\) und \(R_{sq2}\) so, dass \(U_{out}\) der gesuchten Vorspannung aus Kapitel 5.3 entspricht.
\[U_{out} = \mathtt{\text{1.35}} \ \mathtt{\text{V}}\]
Der maximale Laststrom der Vorspannungsquelle \(I_{LmaxVvor}\) wurde in Kapitel 5.3 bestimmt, indem der maximale Strom der Vorspannungsquelle im Betrieb mittels Simulation bestimmt wurde und mit einer gewissen Sicherheit aufgerundet wurde.
\[I_{LmaxVvor} = \mathtt{\text{500}} \ \mathtt{\text{uA}}\]
Die Berechnung von Transistorschaltungen erfolgt immer mit gewissen Annahmen. Eine exaktere und damit kompliziertere Berechnung ist nicht sinnvoll, da die Bauteiltoleranzen und Temperatureinflüsse zu groß sind. Folgende Faustregeln gelten für die Berechnung:
\[ I_{1} = I_{2} + I_{B} \tag{5.1}\]
\[ I_{B} = \frac{I_{C}}{100} \tag{5.2}\]
\[ I_{Spg} = 20 I_{LmaxVvor} \tag{5.3}\]
\[I_{Spg} = \mathtt{\text{10}} \ \mathtt{\text{mA}}\]
\[U_{BE} = \mathtt{\text{700}} \ \mathtt{\text{mV}}\]
Mit Maschengleichung 1 \(M_1\) erhält man den Zusammenhang zwischen \(U_2\) und \(U_{BE}\).
\[ 0 = - U_{2} + U_{BE} \tag{5.4}\]
\[ U_{2} = U_{BE} \tag{5.5}\]
\[U_{2} = \mathtt{\text{700}} \ \mathtt{\text{mV}}\]
Mit Maschengleichung 2 \(M_2\) lässt sich \(U_1\) berechnen.
\[ 0 = U_{1} + U_{2} - U_{out} \tag{5.6}\]
\[ U_{1} = - U_{2} + U_{out} \tag{5.7}\]
\[U_{1} = \mathtt{\text{650}} \ \mathtt{\text{mV}}\]
\(I_1\) kann aus dem Knoten 2 berechnet werden, indem Gleichung 5.10 eingesetzt wird.
\[ 0 = I_{1} - I_{2} - I_{B} \tag{5.8}\]
\[ I_{1} = I_{2} + I_{B} \tag{5.9}\]
\[ I_{2} = 10 I_{B} \tag{5.10}\]
\[ I_{1} = 11 I_{B} \tag{5.11}\]
Wird nun noch Gleichung 5.16 in Gleichung 5.11 eingesetzt, erhält man eine Gleichung für \(I_1\) in Abhängigkeit von \(I_C\).
\[ I_{1} = \frac{11 I_{C}}{100} \tag{5.12}\]
Über den Knoten 1 wird der Zusammenhang zwischen den Strömen dargestellt. Für \(I_L\) muss der maximale Lastrom eingesetz werden. Dieser kann aus einer Transientensimulation in Kapitel 5.3 ermittelt werden. Der Strom \(I_{spg}\) kann mit der Faustregel Gleichung 5.3 bestimmt werden. Werden diese Informationen und Gleichung 5.17 in Knoten 1 Gleichung 5.13 eingesetzt, kann durch Umformen \(I_c\) berechnet werden.
\[ 0 = - I_{1} - I_{C} - I_{L} + I_{Spg} \tag{5.13}\]
\[ 0 = - \frac{111 I_{C}}{100} + 19 I_{LmaxVvor} \tag{5.14}\]
\[ I_{C} = \frac{1900 I_{LmaxVvor}}{111} \tag{5.15}\]
\[I_{C} = \mathtt{\text{8.56}} \ \mathtt{\text{mA}}\]
Durch Einsetzen der Zahlenwerte können nun \(R_{sq1}\) und \(R_{sq2}\) berechnet werden.
\[ I_{B} = \frac{I_{C}}{100} \tag{5.16}\]
\[I_{B} = \mathtt{\text{85.6}} \ \mathtt{\text{uA}}\]
\[ I_{1} = 11 I_{B} \tag{5.17}\]
\[I_{1} = \mathtt{\text{941}} \ \mathtt{\text{uA}}\]
\[ R_{sq1} = \frac{U_{1}}{I_{1}} \tag{5.18}\]
\[R_{sq1} = \mathtt{\text{690}} \ \mathrm{\Omega}\]
\[ I_{2} = 10 I_{B} \tag{5.19}\]
\[I_{2} = \mathtt{\text{856}} \ \mathtt{\text{uA}}\]
\[ R_{sq2} = \frac{U_{2}}{I_{2}} \tag{5.20}\]
\[R_{sq2} = \mathtt{\text{818}} \ \mathrm{\Omega}\]
Wird der Spannungsteiler aus \(R_{sq1}\) und \(R_{sq2}\) als unbelastet betrachtet, indem sichergestellt wird, dass \(I_1 >> I_B\) ist, vereinfacht sich die Berechnung erheblich. Allerdings sind damit auch höhere Ruheströme und damit Verluste verbunden.
5.4.2 Überprüfen und einstellen mittels Simulation
Nun wird mittels Simulation die Berechnung überprüft und die Schaltung exakt eingestellt. Zur Überprüfung wird eine “OP” (Operating Point) Simulation verwendet. Um die Schaltung einzustellen, kann eine “DC-Sweep” Simulation, wie dies zum Beispiel in Kapitel 5.3 zur Bestimmung der korrekten Vorspannung gemacht wurde, verwendet werden.
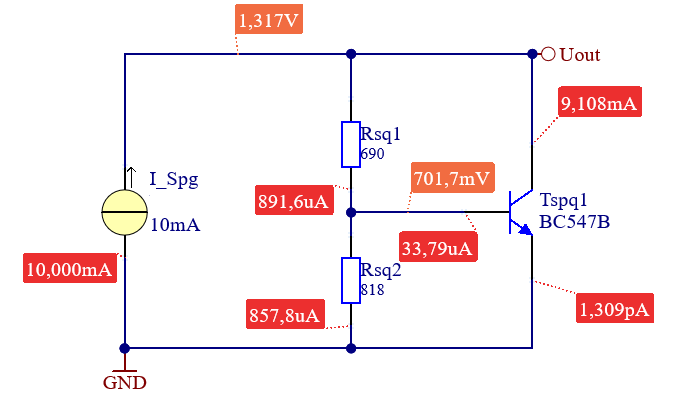
Werden die oben berechneten Werte mittels Simulation überprüft, erhält man eine gute Übereinstimmung für \(U_{out}\). Um eine noch Bessere Übereinstimmung zu erzielen, können die Widerstände mittels DC-Sweep eingestellt werden. Dazu wird \(R_{sq1}\) laut Berechnung gewählt und Widerstand \(R_{sq2}\) “gesweept”. Ziel ist es, den Widerstandswert \(R_{sq2}\) so zu bestimmen, dass \(U_{out}\) den notwendigen Wert der Vorspannung hat, welcher in Kapitel 5.3 mittels “DC-Sweep” ermittelt wurde.
\(U_{out} = 1.35 \ \mathrm{V}\).
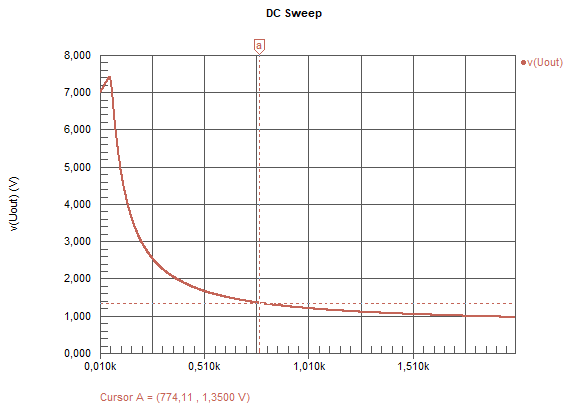
| Simulationsparameter | Wert | Bemerkung |
|---|---|---|
| \(R_{sq2}\) Sweep Bereich | \(1 \ \Omega\) bis \(20 \ \mathrm{k \Omega}\) in \(100 \ \Omega\) Schritten |
| Simulationsergebnis | Wert | Bemerkung |
|---|---|---|
| \(R_{sq2}\) bei \(U_{out} = 1,35 \ \mathrm{V}\) | \(R_{sq2} = 774,11 \ \Omega\) |
Eine neuerliche Simulation bestätigt das Ergebnis.
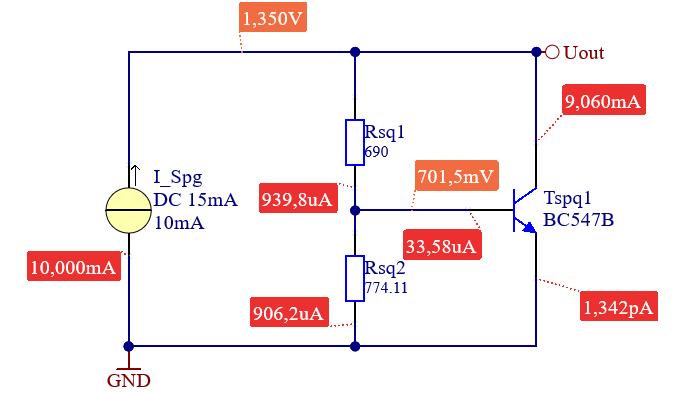
5.4.3 Aufbau
Ist aus dem Schaltungsaufbau zu erwarten, dass Bauteiltoleranzen und Umgebungsbedingungen (z.B. Temperatur) eine Rolle spielen, müssen Potentiometer in der realen Schaltung vorgesehen werden, um diese Effekte zu kompensieren. Beim \(U_{BE}\)-Vervielfacher würde \(R_{sq2}\) als Trimpotentiometer ausgeführt werden. Außerdem ist zu beachten, dass für einen realen Aufbau Widerstandswerte aus den E-Reihen zu wählen sind!
5.4.4 Reale Spannungsquelle in der Schaltung
Der zuvor dimensionierte \(U_{BE}\)-Vervielfacher kann nun in die Schaltung eingebaut werden.
Es gilt aufs neue die Qualität zu überprüfen. Dabei werden die selben Parameter wie in Kapitel 5.3 zur Beurteilung heran gezogen. Zuerst wird wieder eine Operating Point Analyse (OP) durchgeführt um den Arbeitspunkt zu kontrollieren, Abbildung 5.13. Bereits hier ist zu erkennen, dass die gewünschte Vorspannung nicht erreicht wird.
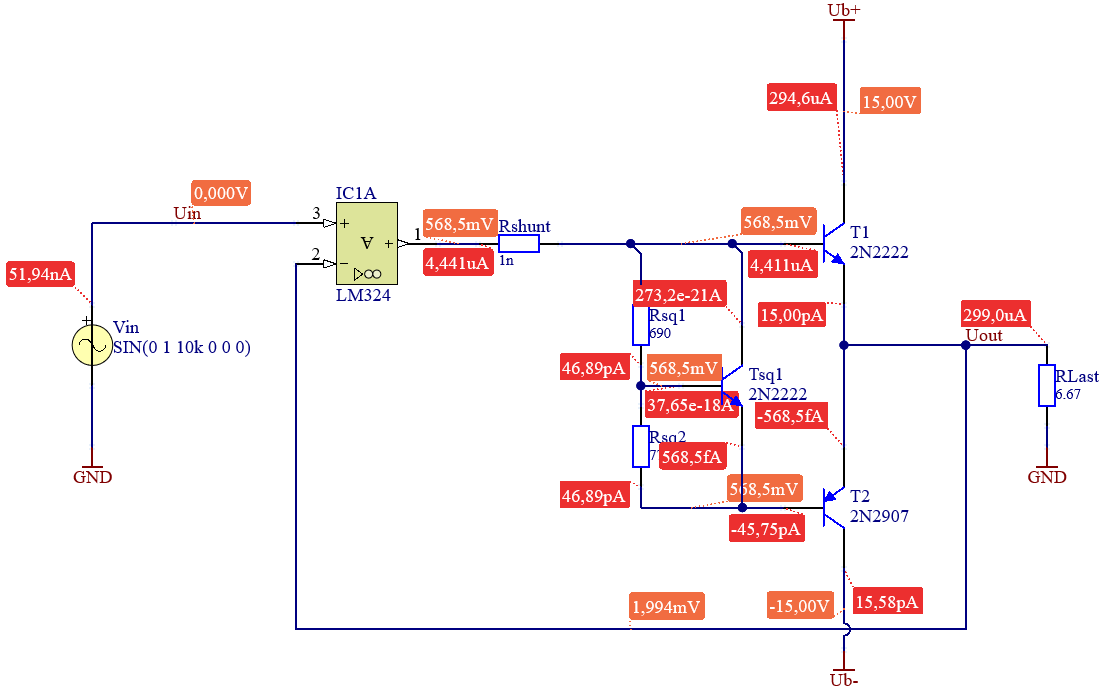
| Simulationsparameter | Wert | Bemerkung |
|---|---|---|
| \(V_{in}\) Frequenz | 10 kHz | |
| \(V_{in}\) Amplitude | 1 V | |
| Simulierte Perioden | 3 |
In der Simulation über die Zeit, der Transientensimulation, sind auch eindeutig die Übergabeverzerrungen zu sehen. Der Grund dafür liegt in der fehlenden Stromversorgung der Spannungsquelle.
Welche noch kostengünstigere Variante zur Realisierung der Vorspannung mit Dioden gibt es? Welchen Nachteile hat diese Lösung? Warum wird nicht einfach eine Stromquelle mit einem Widerstand zur Vorspannung genutzt?
5.5 Stromversorgung
Wie in Kapitel 5.4.4 Simulationsergebnis Abbildung 5.13 und Abbildung 5.14 sichtbar ist, reicht der Ausgangsstrom des OPV’s nicht aus um die reale Vorspannungsquelle zu versorgen. Daher müssen zusätzliche Stromquellen eingebaut werden. Da der Verstärker symetrisch aussteuert, müssen zwei Stromquellen eingebaut werden. Eine für die negative und eine für die positive Versorgung.
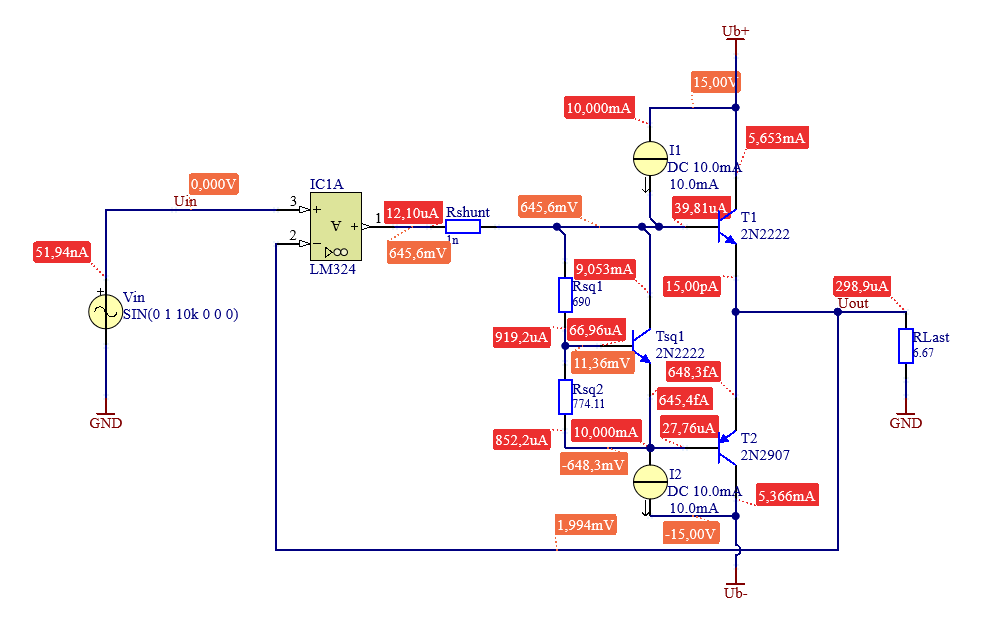
Mittels Arbeitspunktsimulation ist zu sehen, dass die Vorspannung durch den Einbau der Stromquellen erreicht wird. Die Höhe des Stromes richtet sich nach der Dimensionierung von \(I_{spqg}\) in Kapitel 5.4.1.
| Simulationsparameter | Wert | Bemerkung |
|---|---|---|
| \(V_{in}\) Frequenz | 10 kHz | |
| \(V_{in}\) Amplitude | 1 V | |
| Simulierte Perioden | 5 |
Die Verzerrungen sind wieder auf dem Niveau aus Kapitel 5.3 und damit akzeptabel. Nun müssen nur noch die idealen Stromquellen mit realen ersetzt werden.
5.6 Reale Stromquelle
Als geeignete Stromquellen bietet sich der sogenannte Stromspiegel an. Dieser kann wieder analytisch berechnet werden nach [2, pp. 157] oder mittels DC-Sweeps des Widerstandes bestimmt werden. Zur Simulation eignen sich als Last Spannungsgesteuerte Spannungsquellen.
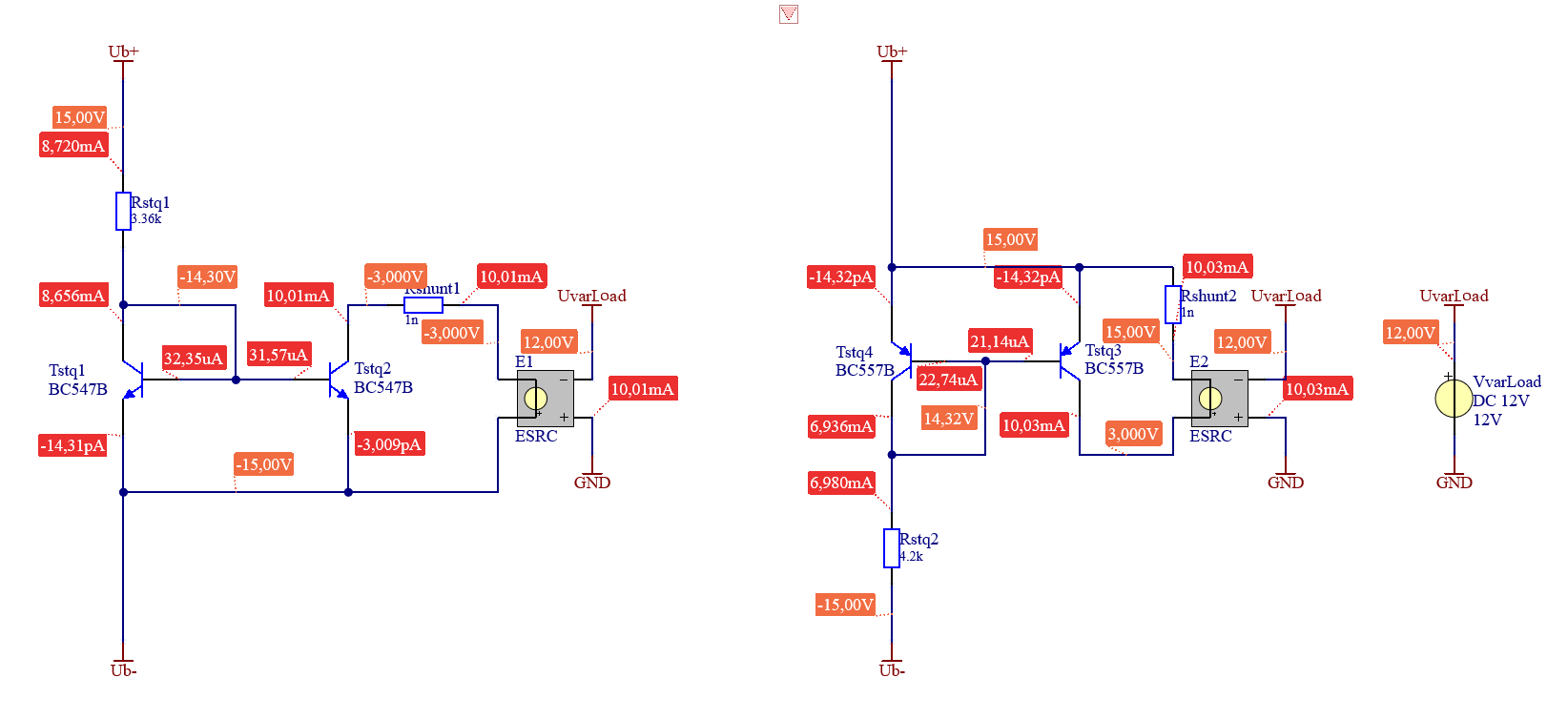
Die Stabilität der Stromquelle kann ermittelt werden, indem die Lastspannung “gesweept” wird. Dabei soll der Verlauf des Stromes möglichst horizontal und konstant sein.
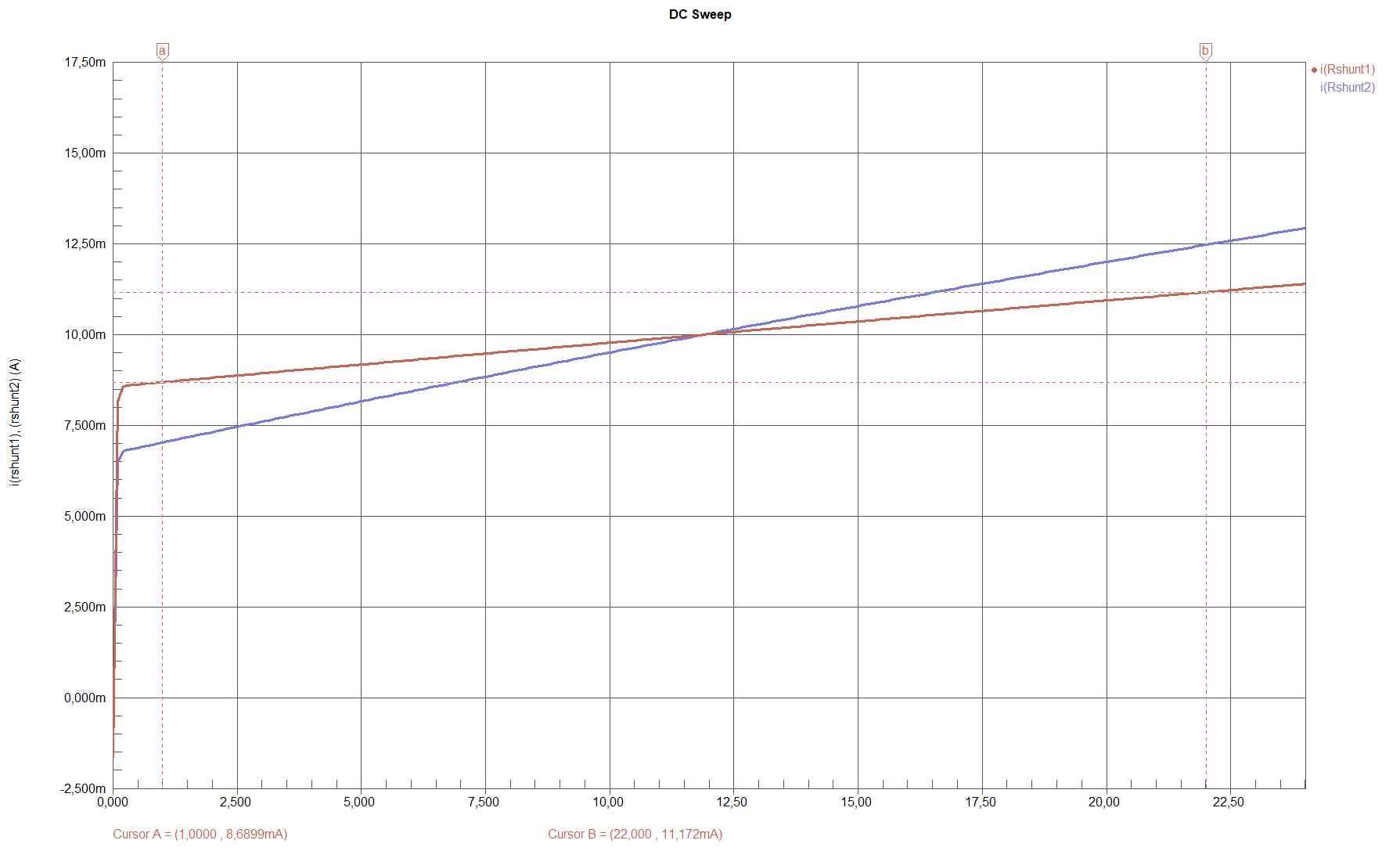
Nachdem die ausreichende Stabilität gezeigt wurde, können die Stromquellen eingebaut und die gesamte Schaltung auf ihre Qualität überprüft werden.
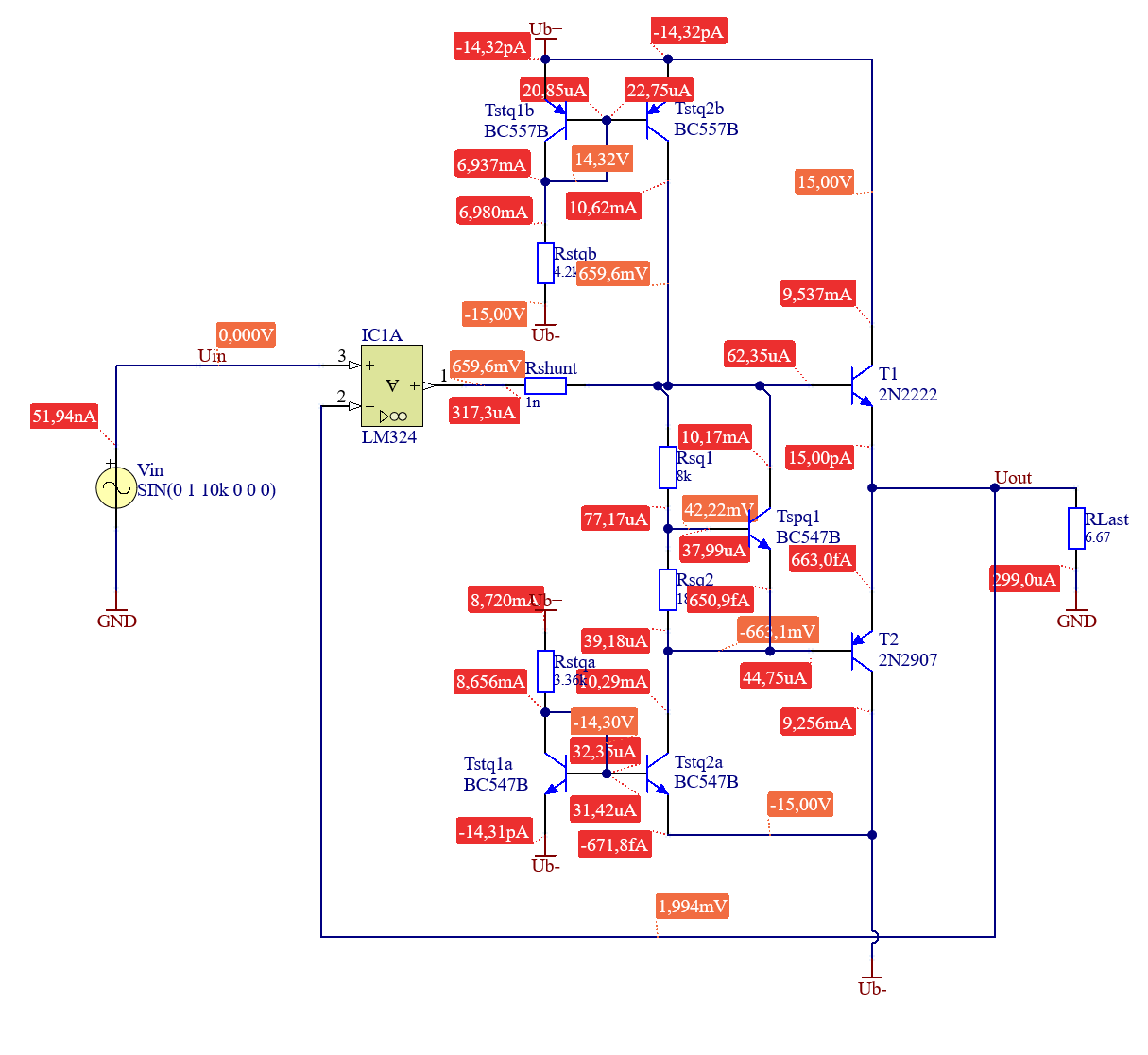
| Simulationsparameter | Wert | Bemerkung |
|---|---|---|
| \(V_{in}\) Frequenz | 10 kHz | |
| \(V_{in}\) Amplitude | 1 V | |
| Simulierte Perioden | 5 |
Vergleicht man nun Ergebnis Abbildung 5.8, bei welchem die Vorspannung ideal ausgeführt wurde, und das Ergebnis Abbildung 5.20 mit realen und damit tatsächlich fertigbar Quellen, ist die Qualitätsunterschied zu vernachlässigen. Die Schaltung gilt damit als fertig dimensioniert. Natürlich kann die Schaltung erweitert, adaptiert und verbessert werden. Siehe dazu Kapitel 5.9.
5.7 Strombegrenzung
Um die Schaltung im Kurzschlussfall zu schützen, kann eine Strombegrenzung eingebaut werden [2], Abb. 18.30 c . Die Strombegrenzung besteht aus einem Widerstand und einem weiteren Transistor Abbildung 5.21.
Die Widerstände \(R_{sb1}\) und \(R_{sb2}\) werden so dimensioniert, dass beim erreichen des maximal erlaubten Stroms durch die Transistoren \(T_1\) und \(T_2\), die Spannung zwischen Basis und Emitter der Transistoren \(T_{sb1}\) und \(T_{sb2}\) so groß ist, dass diese zu leiten beginnen. Damit wird die Basis-Emitter Strecke der Transistoren \(T_{1}\) und \(T_2\) kurzgeschlossen und der Stromfluss unterbrochen.
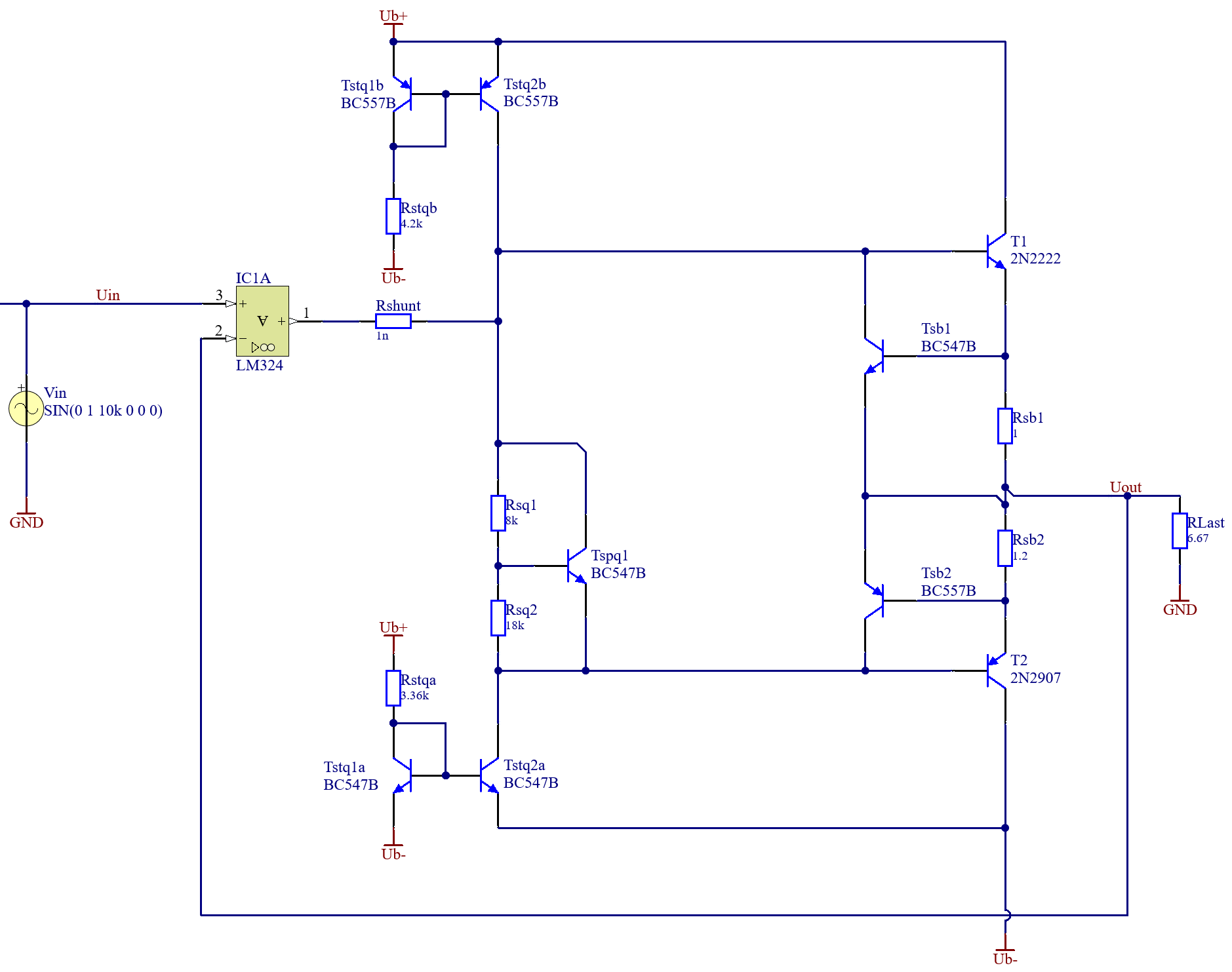
Die Berechnung der Widerstände kann vereinfacht durch die Annahme erfolgen, dass die Spannung \(U_{BE}\) der Transistoren \(T_{sb1}\) und \(T_{sb2}\) größer \(0,7 \ \mathrm{V}\) sein muss um zu leiten.
\[U_{BE,Tsb} = \mathtt{\text{700}} \ \mathtt{\text{mV}}\]
\[I_{T1,max} = \mathtt{\text{800}} \ \mathtt{\text{mA}}\]
\[I_{T2,max} = \mathtt{\text{600}} \ \mathtt{\text{mA}}\]
\[ R_{sb1} = \frac{U_{BE,Tsb}}{I_{T1,max}} \tag{5.21}\]
\[R_{sb1} = \mathtt{\text{875}} \ \mathrm{m\Omega}\]
\[ R_{sb2} = \frac{U_{BE,Tsb}}{I_{T2,max}} \tag{5.22}\]
\[R_{sb2} = \mathtt{\text{1.17}} \ \mathrm{\Omega}\]
Die Widerstände \(R_{sb1}\) und \(R_{sb2}\) werden zum nächsten Wert der E12 Reihe ausgewählt und die Schaltung mittels Simualtion überprüft.
Es ist gut zu erkennen wie die Ströme durch die Transistoren \(T_1\) und \(T_2\) korrekt begrenzt werden. Nun gilt es, mittels Simulation, nachzuweisen, dass die Schaltung auch im Normalbetrieb noch funktioniert.
Werden die Werte mit Strombegrenzung Abbildung 5.23 mit den Werten ohne Strombegrenzung Abbildung 5.20 verglichen, ist zu erkennen, dass die Schaltung eine leicht höhere Abweichung zwischen Eingangsspannung und Ausgangsspannung aufweist. Ob die Abweichung akzeptabel ist, muss im Einzelfall entschieden werden. Für unsere Zwecke stellen wir fest, dass die Schaltung nach wie vor das Signal in ausreichender Qualität verstärkt.
Somit ist festzuhalten, dass die erweiterung um die Strombegrenzung lediglich in der Verlustleistung zu Buche schlägt, jedoch keine Auswirkungen auf die Qualität der Verstärkung hat.
5.8 Praktische Herangehensweise
- Welche Last muss versorgt werden?
- Welche Lastströme sind gewünscht?
- Auswahl passender Transistoren in Bezug auf die maximale Werte.
- Definition der Qualitätsparameter, z.B. Differenz der Ein- und Ausgangspannungen, Oberwellen Anteile, …
5.9 Abwandlungen und Erweiterungen
Wie könnte die Rückkopplung, welche hier mit einem OPV umgesetzt wurde noch realisiert werden?
Wie könnte die Vorspannung mit Dioden umgesetzt werden?
Wie könnte die Leistung weiter erhöht werden?